
"욕실 타일, 반복 구조가 없다!" 50년만에 수학의 난제 해결
저 위의 사진, 별 거 아닌 것처럼 보이지만, 수학을 잘 아는 사람이 보면 무릎을 칠 만한 도형입니다!
저건 정말 대단한 업적이거든요!
이것은 평면덮기 문제와 연관이 있는데요. 여러분, 대칭이 아닌 도형을 이어붙여 평면을 덮는다는 게 엄청 어렵거든요.
예를 들어 대칭인 도형 중에는 평면을 덮을 수 있는 게 여러 개 있죠. 화장실 바닥 타일처럼 정사각형, 이런 건 쉽습니다. 그쵸?
그럼 또 어떤 게 있을까요. 정삼각형도 되네요. 그리고 벌집처럼 정육각형도 서로 모서리를 대면서 평면을 덮을 수 있습니다.
자, 그 다음은요? 생각해 보십시오. 쉽지 않습니다.
이게 수학자들이 고민한 문제거든요. 그런데 비대칭적인 도형으로 평면을 덮는 건 더 쉽지 않습니다.
비대칭 모양은 서로 다른 두 개의 타일을 이용하거나 해야 비로소 평면을 덮을 수 있죠.
그런데 저 위의 사진을 다시 보십시오. 무려 13각형의 비대칭 도형인데, 서로 매끄럽게 맞물리며 평면을 덮고 있습니다!
실로 대단한 일입니다. 이렇게까지 별 거 아닌 걸로 보이면서, 이렇게까지 대단한 연구 결과는 없을 겁니다 ㅋㅋㅋ
그럼 자세한 내용 보실까요.
눈을 크게 뜨고 봅시다.
이쪽과 저쪽이 같은 듯하면서도 다릅니다.
수학자들이 반복되는 형태 없이 평면을 채울 수 있는 도형을 사상 최초로 발견했습니다. 수학계의 난제를 해결한 순수 학문의 성과이면서도 고강도 신소재를 개발할 길을 연 실용적 가치도 크다는 평가를 받았습니다.
미국 아칸소대의 챔 굿맨-스트라우스(Chaim Goodman-Strauss) 교수 연구진은 지난 20일(현지 시각) 논문 사전 공개 사이트인 아카이브(arXiv)에 “비주기적 타일링(aperiodic tiling)이 가능한 13각형 도형을 처음으로 발견했다”고 밝혔습니다.
연구진은 이 도형의 모양 때문에 ‘모자(the hat)’라는 별명을 붙였습니다. 모자들은 서로 빈틈없이 맞물리며 평면을 가득 채우면서도 반복되는 형태가 나타나지 않았습니다. 또 모자의 각 변의 길이가 달라져도 결과는 같았습니다.
블랙홀 연구자가 창시한 ‘이상한’ 타일
보도블록이나 벽지, 욕실을 보면 단순한 무늬가 반복적으로 이어진 경우가 많습니다. 타일들이 빈틈없이 이어진 것과 같다고 타일링 또는 테셀레이션(tessellation)이라고 합니다. 우리말로 ‘쪽매맞춤’이라고 부릅니다.
여러 도형이 대칭 이동을 반복하며 벽면을 채운 것을 ‘주기적 타일링(periodic tiling)’이라고 합니다. 체스판은 검고 흰 정사각형이 번갈아 있습니다. 한 줄만 건너뛰면 똑같은 무늬가 나옵니다.
연구진은 이번 13각형 모자가 ‘아인슈타인(einstein)’ 도형이라고 했습니다. 상대성이론을 만든 물리학자의 이름이 아니라 독일어로 ‘하나의 돌(ein stein)’이란 뜻이다. 한 가지 도형으로 벽면을 대칭 구조 없이 채웠다는 것입니다.
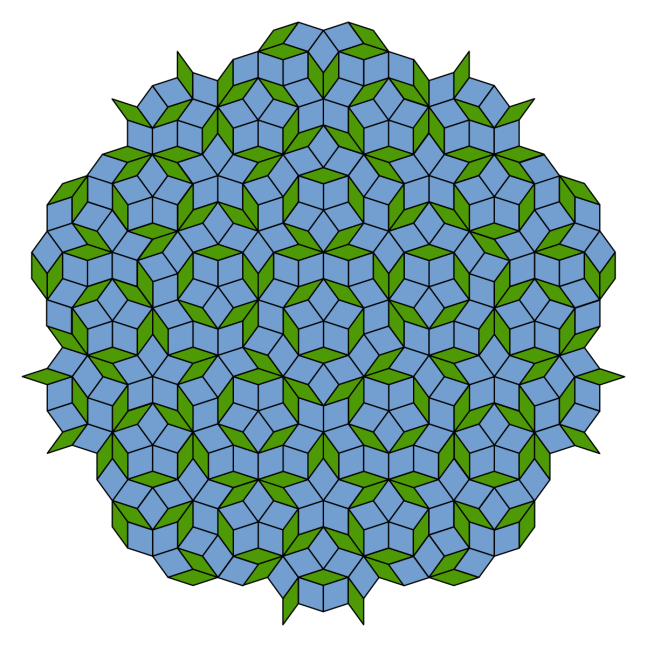
영국의 수학자이자 물리학자인 로저 펜로즈(Roger Penrose)는 1974년 두 가지 다른 모양의 마름모로 비주기적 타일링을 구현했습니다. 단일 도형으로 비주기적 타일링이 구현될 수 있다는 가능성을 제시한 것입니다.
연구진은 두 가지 방법으로 아인슈타인 도형을 증명했습니다. 먼저 13각형 도형을 여러 개 연결한 ‘메타타일(metatile)’들이 모여 다시 더 큰 ‘슈퍼타일(supertile)’을 만들 수 있으며, 이런 과정이 무한히 이어질 수 있음을 확인했습니다. 이런 계층적 구조는 비주기적 타일링의 일반적 모습이라고 연구진은 밝혔습니다. 다음은 13각형 변들의 상대적 길이를 바꿔도 역시 반복되는 형태가 없이 평면을 채울 수 있음을 입증했습니다.
연구진은 비주기적 타일링의 증명은 고성능 컴퓨터와 창의적인 인간의 합작품이라고 밝혔습니다. 굿맨-스트라우스 교수는 “말 그대로 100만개 중 하나를 찾기 위해 99만9999개를 걸러내는 지루한 작업을 해야 하지만 가치가 있다”며 “인간이 이해할 수 있는 증거를 만드는 데 인간이 관여해야 한다”고 말했습니다.
연구진은 앞으로 또 다른 아인슈타인 도형을 찾겠다고 밝혔습니다. 논문 공저자인 캐나다 워털루대의 크레이그 카플란(Craig S. Kaplan) 교수는 “이번에 우리가 문을 열었기 때문에 앞으로 다른 새로운 도형이 나올 것”이라고 밝혔습니다.
고강도 신소재 개발 길도 열어
과학계는 이번 연구 결과가 기초 수학 연구의 성과이면서도 응용 가능성도 크다고 봅니다. 주기적 타일링은 결정 구조에서도 나타납니다. 같은 구조가 반복되다 보니 일부 문제가 생기면 결정 구조가 무너집니다. 바로 깨어지는 것입니다. 비주기적 타일링은 이런 문제가 없는 고강도 신소재로 이어질 수 있습니다.
'놀라운 세상' 카테고리의 다른 글
| 韓美 등 공동주최 민주주의 정상회의 개막…29일 정상급 총회 (1) | 2023.03.29 |
|---|---|
| '난자 냉동 시술 지원'서 비혼 여성은 제외 (3) | 2023.03.29 |
| 호주서 아마추어 채굴업자, 금 2.6㎏ 포함된 돌덩어리 횡재 (4) | 2023.03.28 |
| 일본, 사상 최대 1천140조원 예산 확정…방위비 26% 증가(종합) (7) | 2023.03.28 |
| "아이 때문에 총회 참석 어렵다"고 하자 "자퇴하시길"…간호학과 '똥군기' 논란 (5) | 2023.03.28 |


